Тема 2. Способи представлення графів

Способи представлення графів

Для складання алгорит­му розв'язання задачі, яка базується на графах, не важ­ливі геометричні деталі малюнка.

Вважається, що граф однозначно заданий, якщо задані множини його вершин та ребер і вказані всі зв'язки цих еле­ментів графа, тобто відомо, які вершини і якими ребрами з'єднані.

Існує два найпоширеніших способи представлення графів: матрицею суміжності та списком суміжних вершин.

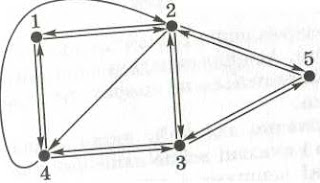
1. Розглянемо граф і представимо його двома способами.

Перший спосіб передбачає задання матриці суміжності, яка для графа з п вершинами представляється двовимірним ма­сивом n*n.

            1       2      3       4      5

1	0	1	0	1	0
2	1	0	1	1	1
3	0	1	0	1	1
4	1	1	1	0	0
5	0	1	1	0	0

Ця матриця суміжності представляє неорієнтований незважений граф, за наявності суміжності вер­шин і та j відповідні елементи матриці дорівнюють 1, тобто а[і, j] = a[j, і] = 1, при відсутності ребра між вершинами і та j відповідні елементи матриці дорівнюють 0, тобто а[і, j] = a[j,і] = 0.

Зауважимо, що для неорієнтованого графа матриця суміжності є симетричною. Значення діагональних елементів дорівнюють 0, оскільки у нашому графі відсутні петлі.

2. Якщо в ор­графі всі суміжні вершини мають двоорієнтовані ребра, то матриця суміжності такого графа збігається з матрицею суміжності для неорієнтованого незваженого графа.

3. Для орієнтованого незваженого графа матриця суміжності не буде симетричною. Оскільки у цьому графі є ребро-петля, то діагональний елемент відповідної вершини рівний 1 (неорієнтований незважений граф теж може містити петлі). Наприклад:

       

  

      
            1       2      3       4      5

1	0	1	0	1	0
2	0	0	1	1	0
3	0	0	0	0	1
4	0	0	1	0	0
5	0	1	0	0	1

4. Розглянемо зважений орграф. Елементи матриці суміжності a[i,j], що описує такий граф, збігатимуться зі значеннями "ваги" ребер між вершинами i та j.

      1         2        3         4         5

1	0	9	0	5	0
2	0	0	1	3	0
3	0	0	0	0	10
4	0	0	3	0	0
5	0	4	0	0	2

Другим способом представлення графа є списки суміжних вершин. Тобто для кожної вершини записується список суміжних вершин, який у довільному порядку містить усі суміжні з нею вершини.

Для графів №1 та №2 задається такий список суміжних вершин:

1 => 2 => 4

2 => 1 => 5 => 3 => 4

3 => 2 =>  4 => 5

4 => 1 =>3 => 2

5 => 3 => 2

Для графа №3:

1 => 2 => 4

2 => 3 => 4

3 => 5

4 =>3

5 => 2=> 5

Для графа №4:

1 => 2(9) => 4(5)

2 => 3(1) => 4(3)

3 => 5(10)

4 =>3(3)

5 => 2(4)=> 5(2)

Перший спосіб нам зрозуміліший, бо обробля­ти елементи матриці суміжності є нескладно. У ній одразу можна дізнатися, чи є дві задані вершини суміжними, чи має граф петлі, яку «вагу» має ребро, що з'єднує дві задані верши­ни.

Однак, наприклад, для неорієнтованих графів, що не мають петель, матриця суміжності містить зайву інформацію, оскіль­ки вона є симетричною. Якщо ж у якості опису графа обрати список суміжних вершин, то значно покращується компакт­ність представлення інформації, однак при цьому втрачається зручність її обробки. Тому спосіб представлення графа обирається автором алгоритму згідно з поставленою задачею.

Завдання

1.  Реалізувати програму, яка по заданих вхідних даних, що описують деякий граф (кількістю вершин, кількістю ребер і пар вершин, які зада­ють ці ребра), створює відповідну матрицю суміжності.

а) задати неорієнтований незважений гра­ф, що не має петель та з кількістю вершин N (наприклад  N = 5), вивівши результат виконання програми у файл.

б) задати орієнтований незважений граф, що не має петель та з кількістю вершин N (наприклад  N = 5), вивівши ре­зультат виконання програми у файл.

в) задати неорієнтований зважений граф, що не має петель та з кількістю вершин N (наприклад  N = 5), вивівши результат виконання програми у файл.

г) задати орієнтований зважений граф, що має петлі та з кількістю вершин N (наприклад  N=5), вивівши результат виконання програми у файл.

2. Реалізувати програму, яка по заданих вхідних даних, що описують деякий граф (кількістю вершин, кількістю ребер і пар вершин, які зада­ють ці ребра), створює відповідний список суміжних вершин.

    Використати графи із завдання №1 (а, б, в, г).